斜鏡オフセットが無いニュートン鏡筒において周辺減光を均等にする最適位置を考察し、それに基づいて光軸調整をしてみました。
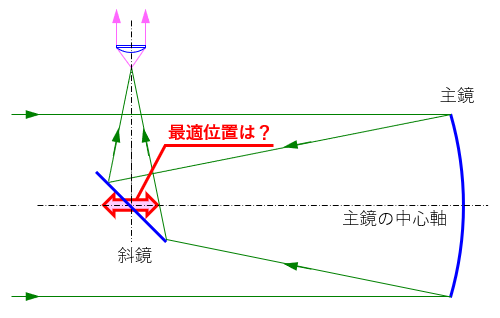
光軸調整において、斜鏡の位置はこの図に示すように主鏡の中心軸に沿って動かすことができます。
この調整において斜鏡位置はどこが最適なのかを考察してみました。
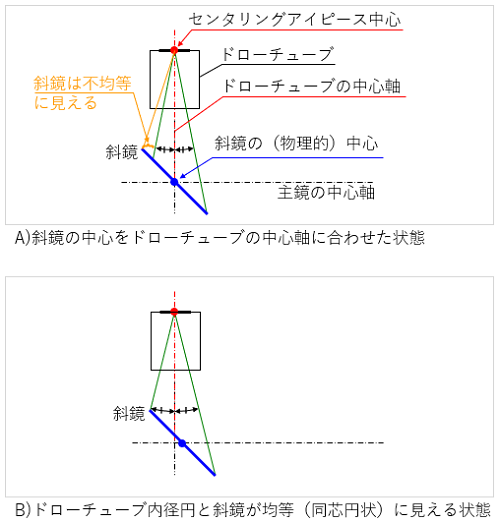
斜鏡の物理的中心(=斜鏡長径の1/2の位置:以降、斜鏡中心と呼称)はオフセット無しの鏡筒の場合は、この図に示すように主鏡の中心軸上にあります。
この斜鏡中心について、A) とB) の2パターン作図してみました。
A) :ドローチューブの中心軸に斜鏡中心を合わせた状態
ニュートン鏡筒の光軸の説明図で多く見られる状態です。この場合、センタリングアイピースから覗くとドローチューブの内径と斜鏡の外径の隙間は不均等で同芯円状には見えません。
理由は、斜鏡の長辺方向の両端に対し、センタリングアイピース中心からの距離が違うためです。この図で左側の斜鏡端はセンタリングアイピースに近く、右端は遠いことが影響しています。
B) :ドローチューブ内径円と斜鏡が同芯円状に見える状態
斜鏡がドローチューブ内径円に対し同芯円状に見えるよう、A) に比べて斜鏡中心を主鏡側へ動かした状態です。
この状態は、周辺減光を均等にする最適位置ではないかと感じますが果たしてそうでしょうか?
考察してみたところ、最適位置は、 最適位置はA) でもB) でもなく、その間 になります。
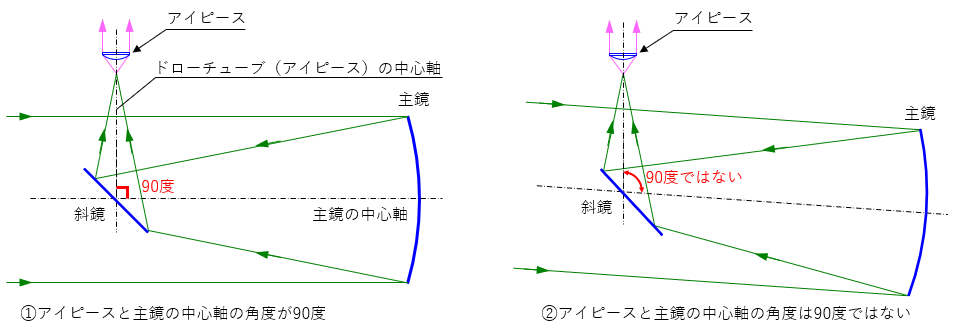
まず光軸があった状態におけるアイピース(ドローチューブ)の中心軸と主鏡の中心軸が成す角度について考えてみました。
以降、アイピース(ドローチューブ)の中心軸を「接眼軸」、主鏡の中心軸を「主鏡軸」と呼称します。
この図に示す①と②はどちらも光軸があった状態(設計通りの結像性能が得られる状態)です。
違いは接眼軸と主鏡軸の成す角度です。
ニュートン鏡筒に置ける副鏡(斜鏡)は平面鏡で、その役割は光路を折り曲げるだけであるため、接眼軸と主鏡軸が重なった状態になるように斜鏡の傾きが調整されていれば、②のように両者の角度が90度でなくても光軸が合っています。
結論を先に述べると、接眼軸と主鏡軸の角度は冒頭で述べた『斜鏡の位置』で決まります。
そのメカニズムを説明します。
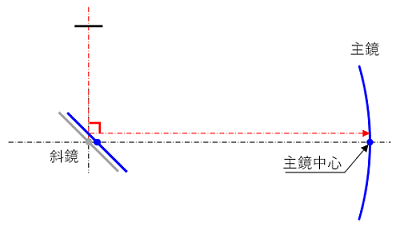
光軸調整の手順に沿って考えると答えが見えてきます。
先ほどの模式図の①の状態(灰色の斜鏡)をから、斜鏡を主鏡方向へ移動してみると(青色の斜鏡)、接眼軸の延長線が主鏡に重なる位置は、主鏡中心より少し上になります。
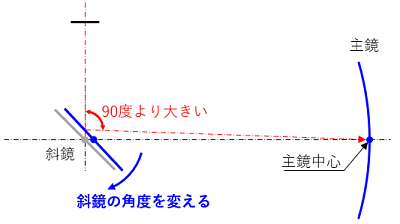
この状態で光軸を合わせるには斜鏡の角度を少し変えてやる必要があり、接眼軸の延長線が主鏡の中心に重なる状態では、接眼軸と主鏡軸は直角より少し大きい角度になります。
(灰色の斜鏡の角度を変えて、青色の状態に変えました)
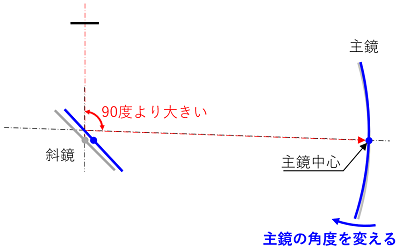
あとは主鏡軸(黒の一点鎖線)が接眼軸(赤の一点鎖線)に重なるように主鏡の角度を変えると光軸があった状態になります。
このように、斜鏡中心を接眼軸上からずらした状態で光軸を合わせると、必然的に斜鏡の軸と主鏡の軸が直交しない状態になるわけです。
冒頭で記述したように、斜鏡オフセットが無いニュートン鏡筒において周辺減光を均等にすることが、今回の最適化の定義です。
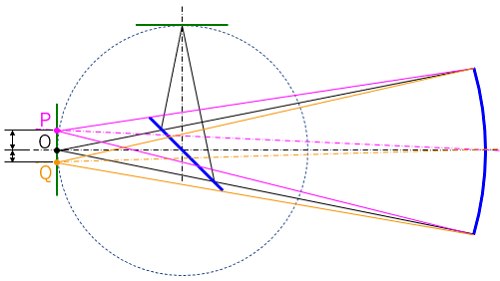
図を用いて説明します。
主鏡の焦点面(緑線)において、主鏡に垂直入射した光線の焦点位置をOとします。Pは斜鏡の上端(主鏡から遠い端)側でのケラレ限界となる時の焦点位置、Qは逆に斜鏡の下端でのケラレ限界となる時の焦点位置です。つまり焦点面でPとQを通る円が斜鏡でのケラレが生じないイメージサークルとなります。
斜鏡の最適位置は、このイメージサークルの中心がOと重なる状態、つまりOP=OQとなる状態と言えます。
| 〜鏡筒の諸元〜 | |
|---|---|
| 主鏡径 D[Φmm] | 200 |
| 焦点距離 fl[mm] | 1,200 |
| 光軸折曲距離 fs[mm]※注1 | 273.5 |
| 斜鏡長径 ds[Φmm] | 88 |
| ※注1.ラフ計測した値です。 | |
タカハシMT-200を対象に具体的な計算結果を表に示します。
(O, P, Qの定義が「斜鏡の最適位置の定義」での説明と少し異なりますので、ご注意下さい)
| 〜斜鏡位置とイメージサークルP、Qの計算結果〜 | |||
|---|---|---|---|
| ★最適斜鏡位置 | A) 斜鏡中心と光軸中心が同一 | B) ドローチューブ内径と斜鏡外径が同芯円状 | |
| 光軸オフセット δ[mm] | 2.3 | 0.0 | 3.5 |
| センターマークオフセット δs[mm] | 3.3 | 0.0 | 4.9 |
| 光軸中心 O[mm] | 3.0 | 0.0 | 4.5 |
| 上イメージサークル半径 P[mm] | 10.5 | 13.7 | 8.9 |
| 下イメージサークル半径 Q[mm] | 10.5 | 7.7 | 11.9 |
この結果より、斜鏡にδsが3.3mmとなるようセンターマークをつけて、そのマークが光軸中心になるように調整すれば最適斜鏡位置にできることがわかました。
計算ツールをエクセルで作りましたので、ご興味ある方はダウンロードしてお使い下さい。
⇒newton_calc_v2.xlsx
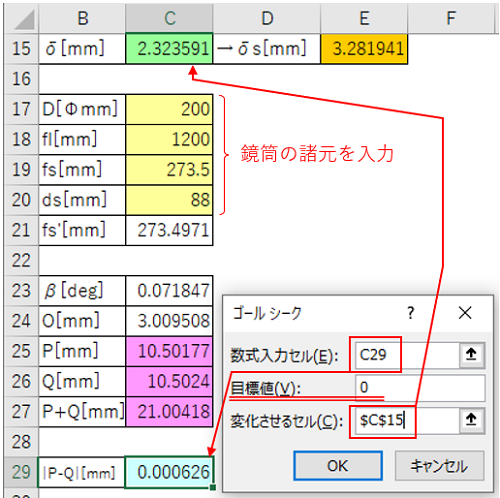
C17〜C20のセル(黄色)に鏡筒の諸元を入力します。
メニューバーより「データ」を選択し、「What-If分析」→「ゴールシーク」を選択します。
数式入力セルは「C29」を選択し、変化させるセルは「C15」を選択して、目標値は「0」を入力して「OK」をクリックします。
適切な値に収束しないときはC15に初期記述している値を適当に変えて、ある程度C29の値を0に近づけてから 再度ゴールシークしてみてください。
ゴールシークが成功したら、C15の値が光軸オフセット δ、E15の値がセンターマークオフセット δsです。
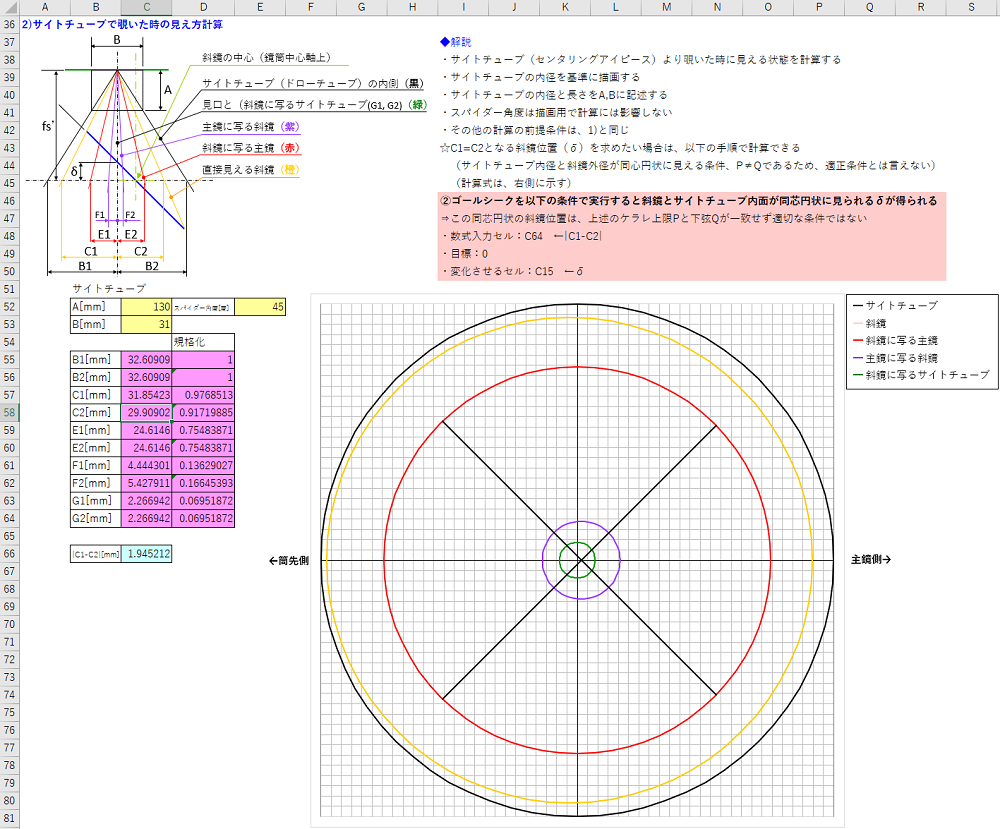
36行目以降で、センタリングアイピースから覗いた時に見えるサイトチューブ(orドローチューブ)、斜鏡、斜鏡に写る主鏡、主鏡に写る斜鏡、斜鏡に写るサイトチューブを描画しますので、見え方の参考になります。
サイトチューブについては、黄色セル(C52, C53に適切な値を入力してください、またE52セルに0または45の値を入力することでスパイダーの向きを変更できます。

ここまでの計算に基づいて、斜鏡中心から3.3mmオフセットしたセンターマーク描き用のテンプレートをトレーシングペーパーに印刷しました。
参考1→主鏡へのセンターマーク貼り付け(MT-200)
参考2→斜鏡のセンターマーク描き(MT-200)
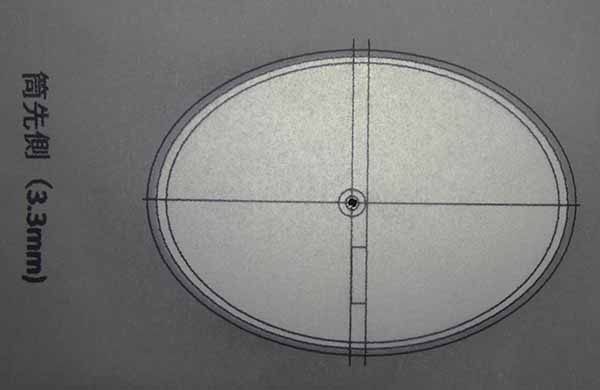
テンプレートに開けた穴を通して、黒マジックでセンターマークを描きました。
(1つ前の写真で作ったテンプレートは外径が合わなかったので、作り直しています。)

センターマークは斜鏡の中心に対し、この写真で左側(筒先側になる方)へ3.3mmオフセットしています。

斜鏡セルに装着しました。

さて、後はこの斜鏡センターマークを頼りに光軸調整をすれば斜鏡が最適位置に調整されます。
接眼部を上にして光軸調整をした結果、斜鏡にオートコリメータを落下させた失敗の反省を活かして、今回は接眼部を横向きにして光軸調整しました。
これ大事です。皆さんも自分だけは大丈夫と思わず、接眼部を横にして光軸合わせをしましょう。
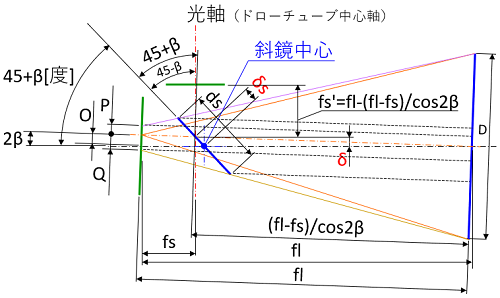
斜鏡の最適位置を計算するために必要な、OとPとQの計算式を説明します。
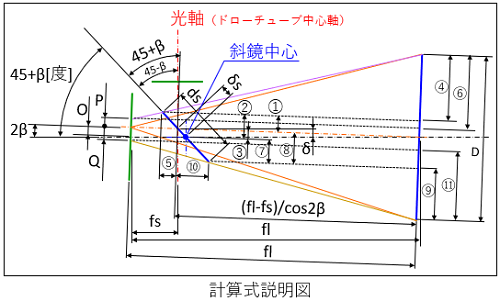
計算の説明図です。

O、P、Qの計算式です。