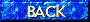暗電流と暗電流によるノイズ
〜ダーク減算で暗電流によるノイズは消せない〜
2022/7/18掲載
2022/7/23更新
はじめに
「ダーク減算」をネットで検索すると、ダークノイズを消す処理であるとの説明が多数出てきます。
これらの説明は、『一部は正解で、一部は不正解(不十分)』だと思います。
このように思う原因は、「ダークノイズ」とは何なのかという定義が曖昧なまま話される(議論される)ことと、天体写真においてはダーク減算では取り除けないノイズも問題になることが根底にあります。
私自身、理解を深めるには時間がかかりましたが、現時点での理解について、「 暗電流とは?」「ダーク減算とは何なのか?」「暗電流によるノイズにはどのようなものがあるのか?」をまとめました。
ダーク減算で消えるものは何か?

ダーク減算無しのダークフレーム
これは、冷却CMOSカメラQHY268M、素子温度+10℃で900秒露光したダークフレーム1コマの中央部付近を拡大した画像、つまりダーク減算していない画像です。
真っ白なホットピクセルや中間色のピクセルがポツポツ散らばった様子が見えます。
この画像はダークフレームですから、一様に真っ黒な画像が本来得られるはずの画像です。こういったピクセルが生じるのはノイズよるものです。
さて、この画像をダーク減算するとどうなるか見てみましょう。
|

ダーク減算後のダークフレーム
同一素子温度、同一露光時間で撮影した別の1コマのダークフレームで減算した画像の同一部分です。
先ほどの画像で目立っていた真っ白のホットピクセルや中間色のピクセルが綺麗に消えました。
さて、ダーク減算で消えたものは何でしょうか?
減算で消えたわけですから、消えたものはいつも同じ場所に同じ明るさ(以降、カウントと呼称)で現れた固定パターンと言えます。つまり、ここで消えたのは、『暗電流のムラ』と『ゼロ点(バイアス)のムラ』による固定パターンノイズです。
この固定パターンノイズのことのみをダークノイズと呼ばれることが多いように思います。
このノイズは暗電流により生じているのですが、実は他にも暗電流により生じるノイズで、綺麗な天体写真を得るために抑制が必要なノイズがあります。
|
他のノイズは含まれていないか?
上記の2枚の画像について、同じ範囲(レンジ:200)にレベルを切り詰めてみました。
ダーク減算無しのダークフレーム
先ほどは見えていなかったピクセル毎の濃淡が見えます。
ヒストグラムを見てみると、平均値を挟んで左右がほぼ均等に分布していることがわかります。
|
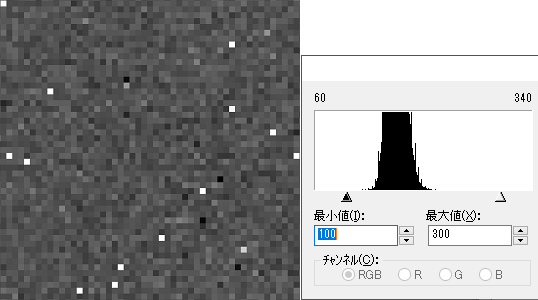
ダーク減算後のダークフレーム
ピクセル毎の濃淡が残っています。しかも、ダーク減算無しの画像と比べて、濃淡の程度が大きくなっているように見えます。
これはヒストグラムに明確に現れており、裾野の幅が明らかに大きくなっています。
ダークフレームを減算によりピクセル毎の濃淡が増えたことから、ダークフレームには固定パターンの他にランダムノイズが含まれていると言えます。これが『暗電流(由来の)ポアソンノイズ』です。
暗電流ポアソンノイズは、
ダーク減算により消えることはなく、逆に増えてしまうのです。
|
ランダムノイズの加算・減算
ダーク減算により暗電流ポアソンノイズが増えたことについて、もう少し深堀してみたいと思います。
先ほど示した二つの画像について、ピクセル毎のカウントの標準偏差を確認してみました。
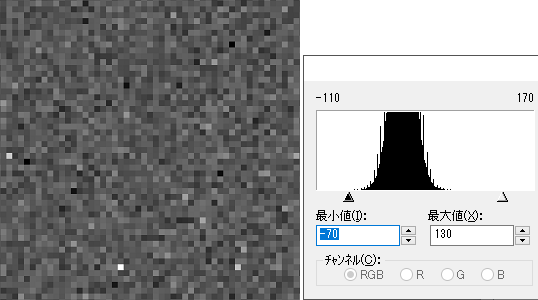
ダーク減算無しのダークフレーム
標準偏差はMakali`iの開口測光を用いて、Star径:1ピクセル、Sky内径:2ピクセル、Sky幅:8ピクセルとし、明るいピクセル(暗電流のムラによるホットピクセル)を避けて求めています。
標準偏差σ:9.9
|
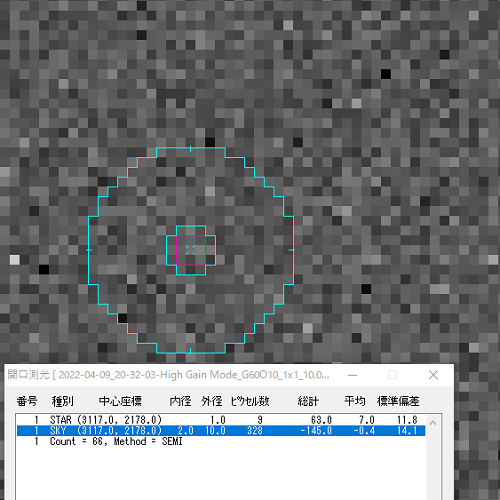
ダーク減算後のダークフレーム
標準偏差σ:14.1
|
ランダムノイズの加算の公式は以下のように表せます。この式から同一のノイズを持つ nコマの画像を加算または減算した場合のランダムノイズの合計の式も求められます。
ランダムノイズは画像の加算だけでなく減算でも増える特徴があります。

今回の場合、ダーク減算後のダークフレームは2コマのダークフレームの減算であることから、上記の公式によると減算前に比べて√2倍になります。
Makali`iを用いて実際に計測した標準偏差は、ダーク減算前が9.9に対し、ダーク減算後で14.1に増加し約√2倍になっています。このようにランダムノイズの公式と良く一致した結果になったことから、ダークフレーム画像に見られたピクセル毎の濃淡はランダムノイズであり、これが暗電流ポアソンノイズと言えると思います。
【補足】
ランダムノイズはダーク減算で増えることから、減算に使用するダークフレームは十分にノイズを低減したもの、つまり十分なコマ数のダークフレームを加算平均したものを使用することが重要とわかります。
暗電流(Dark Current)ポアソンノイズの正体は?
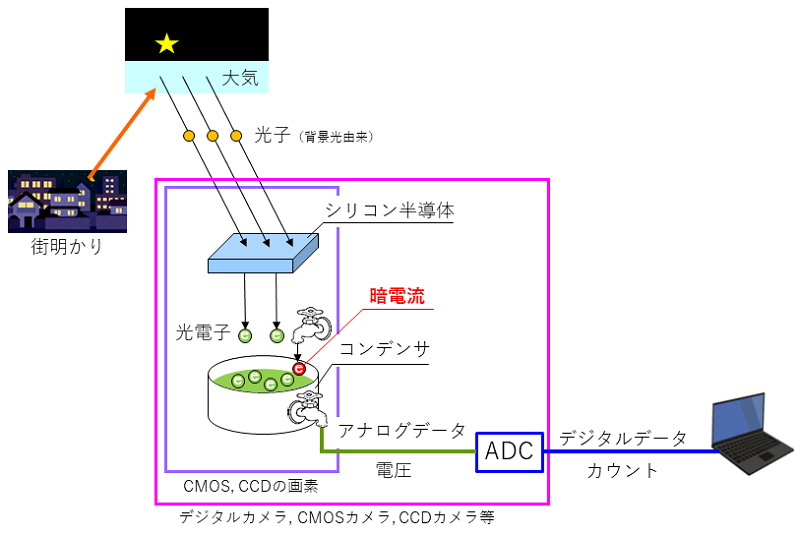
この図は「背景光ノイズとは?」で解説に使ったのと同じデジタルカメラ等の構造の模式図に『暗電流』の説明を加えたものです。
暗電流というのは、CMOSやCCDの各画素のコンデンサに周辺の回路から直接漏れ込む電子のことです。光電子と同じ電子であるため、カメラとしては光と区別できません。
この暗電流による電子も背景光による光電子と同じようにポアソン分布に従ったゆらぎをもって検出されます。この揺らぎが『暗電流(由来の)ポアソンノイズ』です。
つまり、暗電流が大きいと空(背景光)が明るいのと同じことになり、淡い星が見えなくなってしまいます。
暗電流(Dark Current)の特徴について
暗電流(ノイズではなく、暗電流そのもの、つまり暗電流による電子)は、以下の特徴を持ちます。
- 露光時間に比例して増える ⇒ 暗電流の単位は(e-/秒)
- 温度依存性があり、素子温度が高いほど暗電流は大きくなる
この特徴を実際に計測して確認してみました。
計測条件を表1に示します。
表1
| カメラ | QHY268M |
| 読み出しモード | HighGainMode |
| GainSetting | 60 |
| 変換係数1/G値 | 0.297(e-/counts) |
|
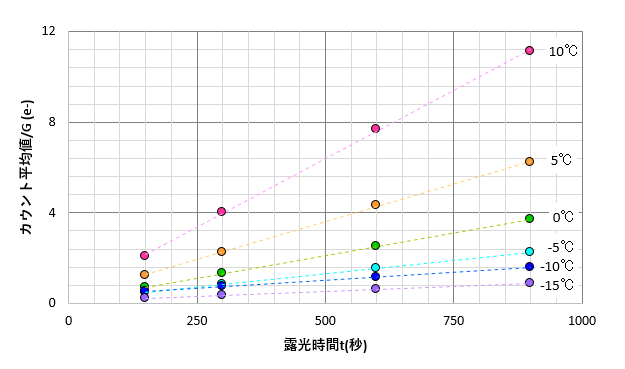
カウント平均値に1/G値を掛けて、(e-)単位に変換したものをプロットしたグラフです。
グラフより言えることは以下の通りです。
| ・ | 同一素子温度のプロットは、露光時間に比例する |
| ・ | 暗電流(e-/秒)は、各素子温度のプロットの傾きである |
| ・ | 暗電流(e-/秒)には温度依存性があり、素子温度が低いほど小さくなる |
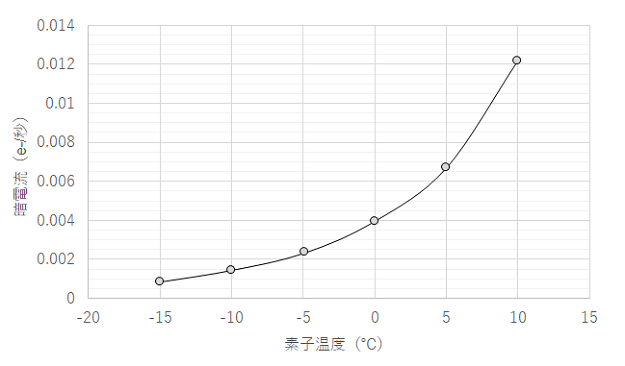
上記の結果を縦軸に暗電流(e-/秒)、横軸に素子温度としてプロットしてみました。
冷却することで、暗電流が十分に下がることがわかります。
まとめ
暗電流によるノイズは表2に示す2つのノイズがある
表2
| 項目 |
原因 |
特徴 |
抑制方法 |
| 暗電流固定パターンノイズ |
- 素子毎の暗電流の違いによるムラ
- ゼロ点(バイアス)のムラ
|
- 同一温度、同一露光時間であれば同じ固定パターンがあらわれる
|
- ダーク減算する(十分なコマ数のダークフレームを使用しないと、暗電流ポアソンノイズが増加する)
- ディザリング撮影&多数コマ加算または加算平均合成する
- ホットピクセル、クールピクセル処理
|
| 暗電流ポアソンノイズ |
- 暗電流電子の検出のゆらぎ
(ポアソン分布に従うランダムノイズ)
|
- 素子温度が低いほどノイズが小さくなる
- 露光時間の平方根(√)に比例して増加する(信号は露光時間に比例して増えるので、合計露光時間を増やすとS/Nが向上する)
|
- 素子を十分に冷却する
- 合計露光時間を十分に伸ばす(ことでS/Nを向上できる)
|
|