ネット上でニュートン鏡筒の光軸調整の手順を検索すると、斜鏡の傾き調整手順が2通り紹介されていることに気づきました。
何が2通りなのかというと、サイトチューブ(タカハシではセンタリングチューブと呼ばれるものと同じ機能、以降「CT」と呼称)を使って斜鏡の傾き調整を行なう時に、何をどこに合わせるかという点です。2つの手順はどちらでも調整できるのか、どちらの手順の方が良いのか、机上検討で考察してみました。
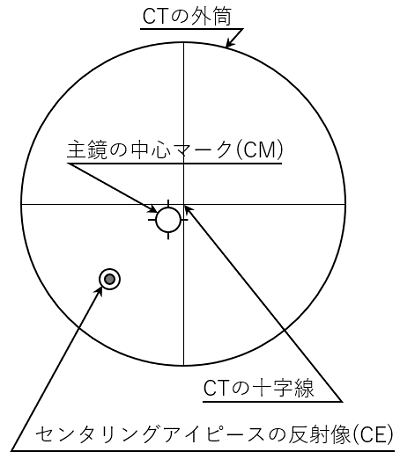
主鏡、斜鏡共に光軸がズレている時に、CTとセンタリングアイピース(CE)(=チェシャアイピース)を使用した場合の見え方です。
CTの外筒の中にCTの十字線があり、その向うに(斜鏡に写る)主鏡と主鏡の中心マーク(CMと呼称)が見えます。また、その主鏡には斜鏡が写り斜鏡の中にセンタリングアイピース(覗き口)(CEと呼称)が見えます。
(注意:この図では、主鏡の外径や斜鏡の外径などの輪郭線、さらに斜鏡を支えるスパイダーは記述していません。)
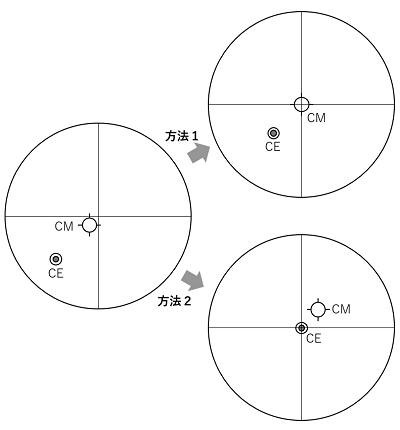
| 何をどこに合わせるのか? | |
|---|---|
| 『方法1』 | CT十字線をCM(主鏡の中心マーク)に合わせる。 |
| 『方法2』 | CT十字線をCE(センタリングアイピースの反射像)に合わせる。 |
Googleで「ニュートン 光軸調整」と検索すると、光軸調整のやり方紹介のページや動画がたくさんでてきます。ざっと数えてみたところ、『方法1』が5例、『方法2』が3例ありました。
タカハシのセンタリングチューブに付属している調整手順は、『方法2』を紹介していて、合わせると『方法1』が5例、『方法2』が4例とほぼ同数になります。
私は長らく、「『方法2』はありえんだろ!」と思っていました。斜鏡の傾き調整は接眼部の光軸(覗き口とCT十字線を結んだ直線)を主鏡の中心に合わせることだと考えています。この考えに従えば『方法1』が自然な選択で、なぜ『方法2』が提唱されているのか理解に苦しんでおりました。
タカハシへ『CT付属の説明書は誤記ではないですか?』と問い合わせたこともあります(おせっかいなやつです(^^;A)。
タカハシからは、「間違いは無いです」との答えがあって、悩みが深まっておりました。
左図に示すCMは斜鏡に1回だけ反射して見えているもので、斜鏡の光軸誤差のみで位置が決まりますが、CEは斜鏡→主鏡→斜鏡という3回の反射を経て見えているもので、斜鏡だけでなく主鏡の光軸誤差も重ね合わせた結果として位置が決まっています。斜鏡の傾きを調整するには、『方法1』が適切としか思えません。
そもそも、『方法2』で光軸が合うのかを検証してみることにしました。
オートコリメータでのニュートン鏡筒の光軸合わせでも紹介しましたが、 沖田様のニュートン反射の光軸修正法に記載されている解析的考察の計算式を利用させてもらいました。
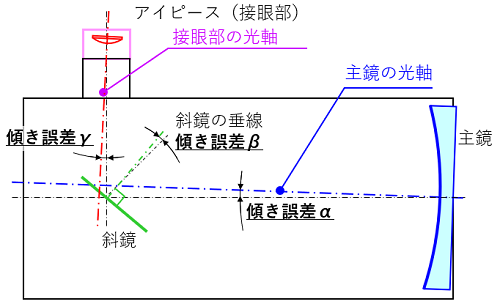
図に示すように、主鏡の光軸の傾き誤差をα、斜鏡の光軸(垂線)の傾き誤差をβ、接眼部の光軸の傾き誤差をγと定義します。
(簡略化のため、計算では左図に示す二次元平面内での誤差のみを考えています)
| ・α: | 主鏡の光軸の傾き誤差 |
| ・β: | 斜鏡の光軸(垂線)の傾き誤差 |
| ・γ: | 接眼部の光軸の傾き誤差 |
| (単位:rad) |
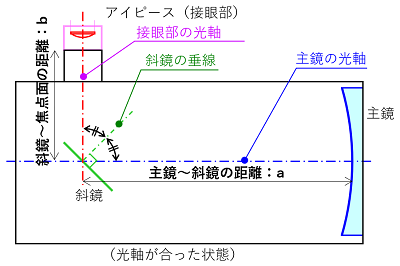
他に計算に必要なパラメータとして、以下の3つを定義します。
| ・f: | 主鏡の焦点距離 |
| ・a: | 斜鏡と主鏡の距離 |
| ・b: | 焦点面と斜鏡の距離 |
| (単位:mm) |
f=a+bの関係になります。
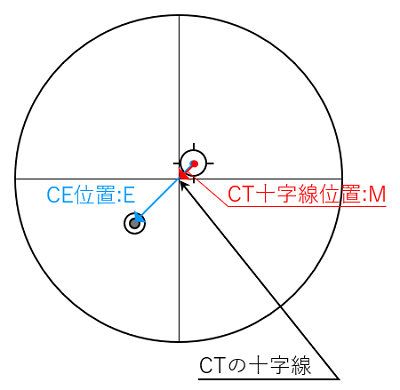
CE&CTを使って覗いた時に見える、CT十字線の位置とCEの位置を主鏡の中心(CM)を基準にして、それぞれM、Eと定義します。
| ・M: | CMを基準にしたCTの十字線交点の位置 |
| ・E: | CMを基準にしたCEの位置 |
M、Eは以下の式で表されます。
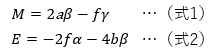
『方法1』は、以下の手順で光軸調整を行ないます。
【手順1】
斜鏡の傾きを調整して、CT十字線をCMに合わせます。
計算式で検討すると、斜鏡の傾き誤差βは、(式1)を用いて、以下のようになります。
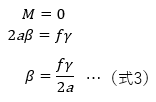
【手順2】
次に主鏡の傾きを調整して、CEをCMに合わせます。
計算式で検討すると、主鏡の傾き誤差αは、(式2)と(式3)を用いて、以下のようになります。
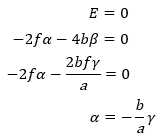
以上の結果より、『方法1』で調整し光軸が合った状態は、以下の式で示すことができます。
【補足】
式中に接眼部の傾き誤差γが残っていますが、光軸調整において基準となるのは接眼部の光軸(今回で言えば、CTの覗き穴と十字線を結んだ直線)で、接眼部の光軸に主鏡の光軸が重なるようαとβを調整することになりますので、α、βにγが含まれるのは、正しいと言えます。
次に『方法2』での光軸調整について、同様の計算を行なってみました。
(2024/5/2:計算式の引用元の沖田様より、『方法2』での計算に誤りがあるとご指摘いただき、計算式を訂正しました。)
『方法1』に比べると計算が複雑ですので、ひとまず結論部分を計算します。
詳細な計算手順は、文末に記載しておきます。
【手順1】n回目の斜鏡の傾き調整
斜鏡の傾きを調整して、CT十字線をCEに合わせます。
1回目の斜鏡の傾き調整→1回目の主鏡の傾き調整→…繰返し…→n回目の斜鏡の傾き調整について記載します。
斜鏡の傾き誤差βnは、以下のようになります。
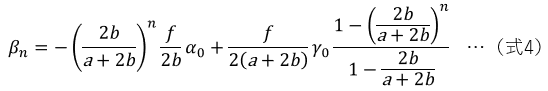
【手順2】
次に主鏡の傾きを調整して、CEをCMに合わせます。
1回目の斜め鏡の傾き調整→1回目の主鏡の傾き調整→…繰返し…→n回目の主鏡の傾き調整について記載します。
計算式で検討すると、主鏡の傾き誤差αnは、以下のようになります。
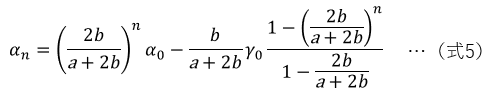
(式4)(式5)について、n→∞の極限を取ると以下のようになります。
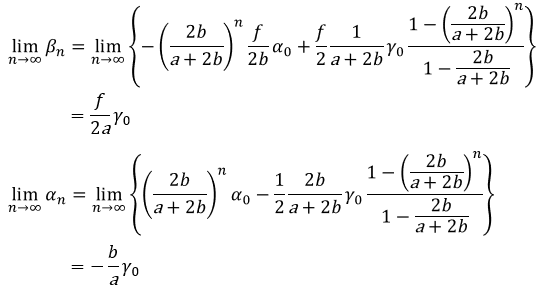
α、βの沿え字は、n回目の調整後ということを示しています。つまりγ0は、γの初期値(光軸調整前)ということを示します。『方法1』のγと『方法2』のγ0は同じです。
以上の結果より、繰返し調整すれば、αとβは以下の式で示すように『方法1』と同じ結果になり、『方法2』も問題なく光軸を合わせられることが分かりました。
タカハシさん、誤記だなんてクレームつけてすみませんm(_ _)m
でもやっぱり、『方法2』はスマートとは思えない。「手間がかかるんじゃないの?」という考えが頭から抜けません。
そこで、具体的な例で、調整回数がどの程度違うのかを検証してみました。
初期の傾き誤差として以下の値を与え、『方法1』と『方法2』で、MとEの値が共に0.2mm以下になるまで計算を行ないました。
| 主鏡の傾き誤差α(deg) | 0.3 |
| 斜鏡の傾き誤差β(deg) | 0.2 |
| 斜鏡の傾き誤差γ(deg) | 0.1 |
この計算検討では、α、β、γは2次元平面で考えておりますので、図中に示すCM,CEの位相は、0-180度方向で示すのが正しいですが、見栄えを意識して、45-225度方向に記述しました
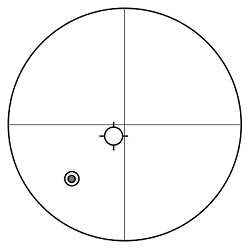
| 十字線の位置M(mm) | 4.4 |
| CEの位置E(mm) | -16.4 |
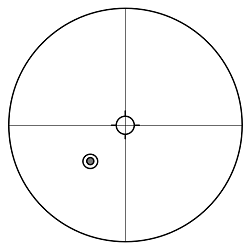
斜鏡の傾きを調整して、CTの十字線をCMに重ねました。
| 十字線の位置M(mm) | 0.0 |
| CEの位置E(mm) | -13.8 |
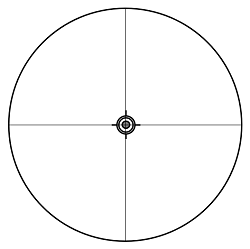
主鏡の傾きを調整して、CEをCMに重ねました。
| 十字線の位置M(mm) | 0.0 |
| CEの位置E(mm) | 0.0 |
以上より、『方法1』では、斜鏡を1回、主鏡を1回の合計2回調整すれば、M=E=0.0となり、光軸が合った状態になることがわかりました。
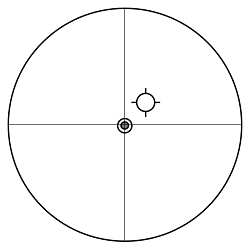
斜鏡の傾きを調整して、CTの十字線をCEに重ねました。
| 十字線の位置M(mm) | -8.7 |
| CEの位置E(mm) | -8.7 |
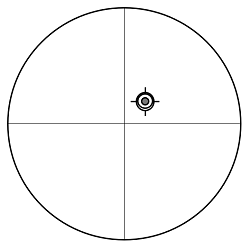
主鏡の傾きを調整して、CEをCMに重ねました。
| 十字線の位置M(mm) | -8.7 |
| CEの位置E(mm) | 0.0 |
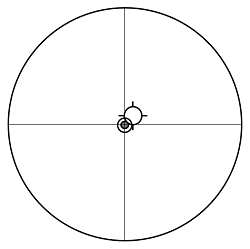
斜鏡の傾きを調整して、CTの十字線をCEに重ねました。
| 十字線の位置M(mm) | -3.2 |
| CEの位置E(mm) | -3.2 |
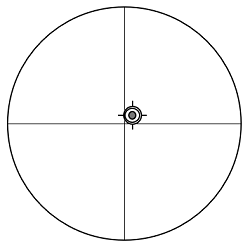
主鏡の傾きを調整して、CEをCMに重ねました。
| 十字線の位置M(mm) | -3.2 |
| CEの位置E(mm) | 0.0 |
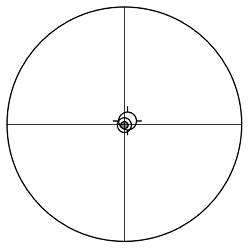
斜鏡の傾きを調整して、CTの十字線をCEに重ねました。
| 十字線の位置M(mm) | -1.2 |
| CEの位置E(mm) | -1.2 |
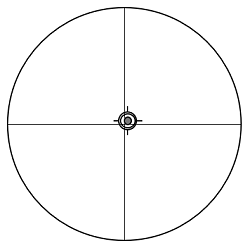
主鏡の傾きを調整して、CEをCMに重ねました。
| 十字線の位置M(mm) | -1.2 |
| CEの位置E(mm) | 0.0 |
斜鏡の傾きを調整して、CTの十字線をCEに重ねました。
| 十字線の位置M(mm) | -0.4 |
| CEの位置E(mm) | -0.4 |
主鏡の傾きを調整して、CEをCMに重ねました。
| 十字線の位置M(mm) | -0.4 |
| CEの位置E(mm) | 0.0 |
斜鏡の傾きを調整して、CTの十字線をCEに重ねました。
| 十字線の位置M(mm) | -0.2 |
| CEの位置E(mm) | -0.2 |
以上より、『方法2』では、斜鏡を5回、主鏡を4回、合計9回の調整で、M=E≦0.2となり、光軸が合った状態になることがわかりました。
言い換えると、『方法2』は『方法1』に比べ、斜鏡、主鏡の調整回数が多く、今回の検討例では合計で7回多く調整する必要があることがわかりました。
以上の検討結果について、横軸に調整回数、縦軸に、MとEの位置をとったグラフを示します。
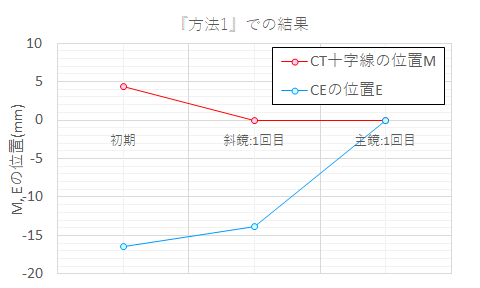
『方法1』での調整回数とMおよびEの変化です。
計算式の(式3)で示されていたように、斜鏡の傾き誤差βの調整において、主鏡の傾き誤差αの影響を受けないため、1回目の斜鏡の調整でM=0.0になっていることで、次の主鏡の調整でM=E=0.0を達成できています。
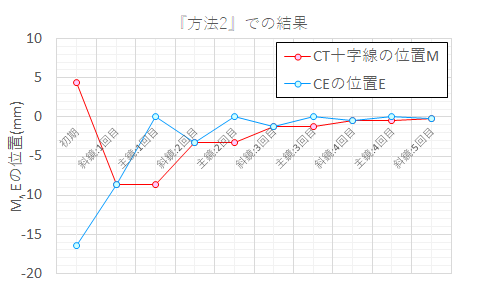
『方法2』での調整回数とMおよびEの変化です。
計算式の(式4)で示されていたように、斜鏡の傾き誤差βの調整において、主軸の傾き誤差αの影響を入っていることで、1回目の斜鏡の調整でMが0.0になりません。そのため、以降の調整でもM=E≒0.0≦0.2に到達するまでに複数回の調整が必要になることがわかりました。
光軸調整の手順は、『方法1』の方が少ない回数で、光軸があった状態に到達できます。調整に使用する指標(見るべきマーク)も同じであり、指標の見えやすさにも違いはありません。
これらの結果より、『方法1』の方が良い調整方法と言えるのではないでしょうか。
『方法2』では、1回で調整が完了しないため、n-1回目の調整結果が、n回目の調整に影響します。
計算式で説明します。
α、β、γの沿え字nは、n回目の調整後の値であることを示します。
斜鏡の傾きを調整して、CT十字線をCEに合わせます。
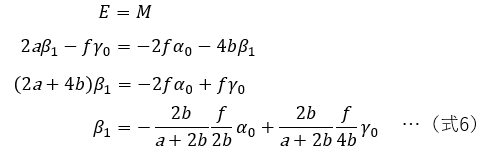
主鏡の傾きを調整して、CEをCMに合わせます。
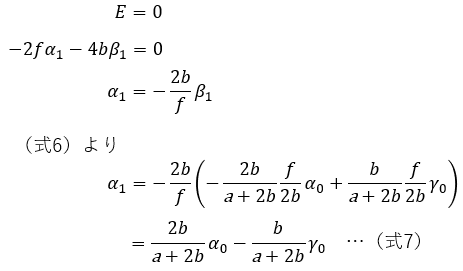
斜鏡の傾きを調整して、CT十字線をCEに合わせます。
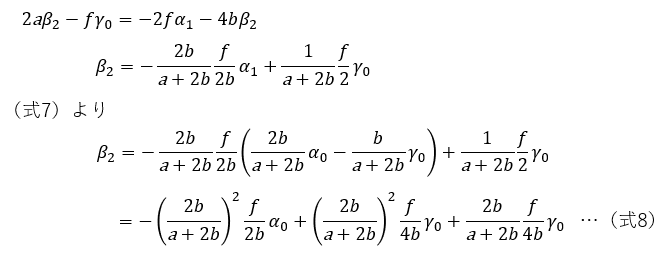
主鏡の傾きを調整して、CEをCMに合わせます。
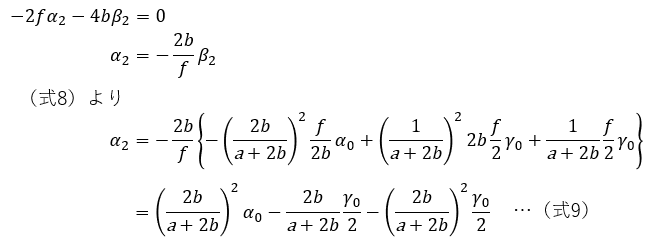
斜鏡の傾きを調整して、CT十字線をCEに合わせます。
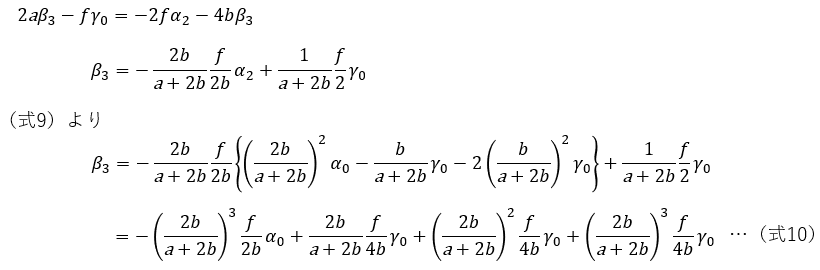
主鏡の傾きを調整して、CEをCMに合わせます。
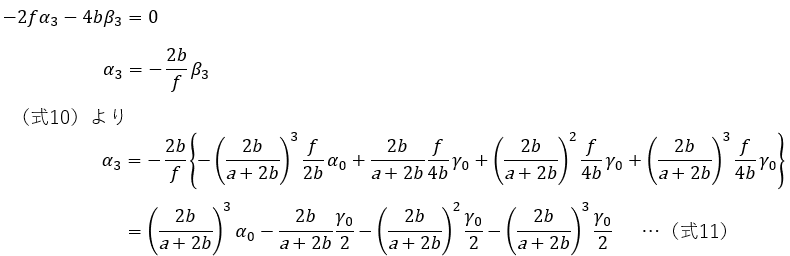
ここまでの計算結果より、n回目の斜鏡および主鏡の傾き調整後のβn、αnは以下のように表せます。
